| 法 規 |
電気通信 システム |
伝送交換設備 及び設備管理 |
線路設備 及び設備管理 |
||||||
| 伝送 | 無線 | 交換 | データ 通信 |
通信 電力 |
通信 線路 |
通信 土木 |
水底 線路 |
||
2016年 3月 18日
◆問題
平成27年度第1回(2015年7月実施)電気通信主任技術者試験の「伝送交換設備及び設備管理」と「線路設備及び設備管理」の 問4 (3)(ⅰ)の過去問です。
出題は、下のとおりです。アンダーラインの部分の(カ)に適した番号を選ぶ問題です。
なお、元の問題は、(3)の問題文と(i)の問題文の2段階になっています。元のままの形では、 ひとつの問題としてのまとまりが悪いので、問題の意味が変わらない程度に文章の配置を換えてあります。ご了承ください。
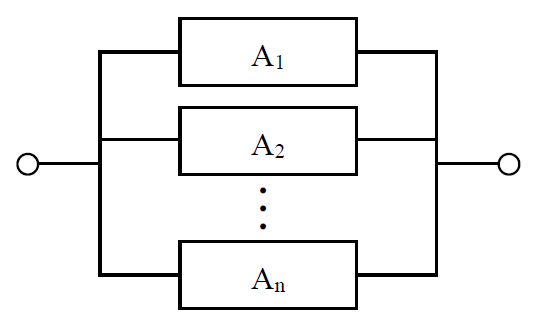
図に示すように、信頼度0.7である装置Aが、n台並列に接続されている1/n冗長システムにおいて、システム全体の信頼度を0.9999以上にするためには、装置Aの台数であるnを少なくとも(キ)以上とする必要がある。 ただし、log10 3 = 0.477 とする。
| ① 6 | ② 8 | ③ 20 | ④ 36 | ⑤ 300 |
◆解答
正解は、② 8 です。
◆解説
◇概要
並列システムの並列数を求める計算問題です。比較的出題頻度が高い問題です。
並列と直列、信頼度と不信頼度の関係が、整理されていないと混乱してしまう問題です。 まだ対数を使う計算があるため、苦手意識を持たれる傾向があります。
対数を使う計算問題の厄介なところは、対数計算そのもののほかに、検算をしにくい点があります。 ここでは、検算代わりの検証方法もご紹介いたします。
◇並列システムの信頼度の公式
1/n冗長システムとは、n個のサブシステムからなるシステムが、1個以上のサブシステムが動作していれは、システム全体が動作する冗長構成です。 つまり、n台の並列システムのことです。
信頼度R1、R2、R3、…の構成要素が並列になっているシステムの信頼度RSは、式(1)で求められます。
RS = 1 - (1 - R1)×(1 - R2)×(1 - R3)×…
この式は、少々複雑に見えますが、不信頼度で考えるとすっきりします。不信頼度Fは、1 - Rです。不信頼度Fを使うと、式(1)は式(2)のようになります。
1 - RS = (1 - R1)×(1 - R2)×(1 - R3)×…
FS = F1×F2×F3×…
今回は、構成要素の不信頼度はすべて同じで、F = 1 - 0.7 = 0.3です。n台の並列とすると、システム全体の不信頼度FSは、式(3)のようになります。
FS = Fn
式(3)の形になると、公式の確認も、やりやすくなります。例えば、(現実的ではありませんが)不信頼度を1/3とします。 これは故障を起こす確率が、1/3ということです。2台並列の場合を考えます。2台並列では、2台が同時に故障しなければ、システム全体は故障となりません。 したがって、システムが故障を起こす確率は、(1/3)2 = 1/9となります。これは、式(3)と一致します。
もし覚えていた公式に不安があったら、このような簡単な数値を入れて確認するのが確実です。 不安なまま計算を進めると、ミスを誘発する原因となります。
◇式を立てる
この問題で求められているのは、要求された信頼度を上回る信頼度を実現する並列台数です。 つまり式(4)を満たす n を求めることです。
要求される信頼度 ≦ n台並列の信頼度
しかしながら、並列のシステムでは式(3)にあるように、信頼度より不信頼度で考えたほうが式が簡単になります。 式が簡単になるということは、それだけミスの原因を減らせるということです。不信頼度で考える場合に求めるものは、 要求された不信頼度を下回る不信頼度を実現する並列台数です。 簡単に言えば、実物の並列システムが故障する確率が、要求レベルより小さければよいのです。
要求される不信頼度 ≧ n台並列の不信頼度
ここまでは、考え方を整理する段階なので、不等号の向きを正確に見てきました。しかし実際の計算では、不等式を使う必要はありません。 不等式ではなく、等号を使った方程式で十分です。なぜかといいますと、nに小数点以下の端数があった場合、切り上げれば良いからです。 言うまでもなく、nは整数です。そして、不信頼度はnが大きいほど小さくなります。これは式(5)から明らかです。したがって、nは大きめにとれば要求は満たされるのです。
ここからは、「nは端数切り上げ」を覚えておき、不等式を使わない方程式でnを求めます。 要求される信頼度をRr、装置1台の信頼度をRとします。そして、不信頼度Fは信頼度RとF = 1 - R の関係があります。 FrとRrの関係も同様です。 これらから、式(3)と式(5)から、式(6)が立てられます。
Fr = Fn
1 - Rr = (1 - R)n
式(6)を満たすnを求めて、端数を切り上げれば、並列台数が求まります。
◇並列台数nを求める。
式(6)から、並列台数nを求めます。問題文から、要求される信頼度をRrは0.9999、装置1台の信頼度をRは0.7です。
1 - Rr = (1 - R)n
1 - 0.9999 = (1 - 0.7)n
0.0001 = 0.3n
ここで、両辺の対数をとります。
log10 0.0001 = log10 0.3n
log1010-4 = log10 [ (3×10-1)n ]
ここから、対数の公式を使います。対数の公式もいろいろとありますが、最低限、指数と対数の関係の式(9)、公式(10)は忘れないでください。
y = ax ⇔ x = logay
loga (x × y) = loga x + loga y
まず式(8)の左辺から、計算します。左辺では、logaxn の計算が必要になります。 もし、この計算に使う公式を覚えていない場合は、式(10)から求めてください。
loga xn = loga (x × x ×… × x)
= loga x + loga x + … + loga x
= n × loga x
したがって、式(8)の左辺は、式(12)のようになります。
log1010-4 = (-4) × log10 10
次は式(12)右辺の log10 10 です。これの公式を覚えていない場合は、対数と指数の関係式(9)に立ち返ります。 log10 10 = ? とすると、式(9)より、
10 = 10の?乗
したがって、?は1なので、式(14)のようになります。
log10 10 = 1
log1010-4 = (-4) × log10 10
= (-4) × 1 ← log10 10 = 1
= -4
なお、公式としては式(16)の形で覚えておくと便利です。この公式は、損失や利得のデシベルを使う問題でも頻繁に使います。
log10 10n = n
次は、式(8)の右辺です。式(11)、式(10)、式(16)より、
log10 [ (3×10-1)n ]
= n × log10 (3×10-1)
←
↑ loga xn = n × loga x
= n × ( log10 3 + log10 10-1 )
←
↑ loga (x × y) = loga x + loga y
= n × ( log10 3 - 1 )
←
↑ log10 10n = n
ここで問題文から、log10 3 = 0.477 なので、
log10 [ (3×10-1)n ]
= n × ( log10 3 - 1 )
= n × ( 0.477 - 1 )
= -0.523 × n
式(8)に戻ります。左辺は式(15)、右辺は式(18)なので、
log10 0.0001 = log10 0.3n
-4 = -0.523 × n
n = 7.6 …
そして、nは端数切り上げなので、n = 8 となります。
◇対数を使わない解法
実は、この問題は手間を惜しまなければ、対数を使わなくても解くことができます。 式(7)を不等式に戻したものを出発点にして、nを求めてみます。なお、不等号の向きは、式(5)からわかります。
0.0001 ≧ 0.3n
対数を使わずに、この式を満たす最小のnを求めます。そのためには、0.3nを実際に計算してみればよいのです。
まずは、n = 2 の場合です。
0.32 = 0.09 ≒ 0.1
したがって、n = 2 では、不等式(20)は成り立ちません。
ここでは、0.32を0.1で近似しています。これは、実際の不信頼度の値よりやや大きめ、不信頼度が大きくなるほうの近似になっています。 つまり正確な不信頼度0.32 は、0.1より小さくなります。そのため、この近似で不等式(20)が成り立てば、正確な値でも不等式(20)は必ず成り立つことになります。
計算を続けます。できるだけ早く不等式(20)を満たすnを見つけるために、次は0.33を計算するのではなく、2乗して0.34を求めます。
0.34 = ( 0.32 )2 ≒ 0.12 = 0.01
n = 4 でも、不等式(20)は成り立ちません。さらに、2乗を求めます。
0.38 = ( 0.34 )2 ≒ 0.012 = 0.0001
これで、n = 8 が、かなり正解に近いことがわかります。0.32 ≒ 0.1の近似は、不信頼度が大きくなるほうの近似なので、 実際の不信頼度はこれより小さくなります。したがって、少なくてもn = 8 で、不等式(20)は近似抜きでも正確に成り立ちます。しかし、求めるべきnは、不等式(20)を満たす最小の値です。まだ、n = 7 以下のときに、不等式(20)が成り立つ可能性が残っています。n = 7 の場合を、計算してみます。
0.37 = 0.36 × 0.3 = ( 0.32 )3 × 0.3
≒ 0.13 × 0.3 = 0.001 × 0.3 = 0.0003
したがって、n = 7 では不等式(20)は成り立ちません。今回の近似の誤差は1割程度なので、0.0003と0.0001の大小関係が逆になる可能性はほぼありません。これで、不等式(20)を満たす最小の値がn = 8と求められます。
しかし、n = 8が正解かどうか、近似の誤差で他の解答にならないか、一抹の不安はあるかと思います。 この不安の正体を整理します。n = 8では、不等式(20)は正確に成り立ちます。したがって不安の正体は、n = 7で不等式(20)が正確に成り立つか、です。 ここで、問題の選択肢を見ると、n = 7はありません。n = 8の下は、n = 6です。0.36を、近似抜きで正確に計算してみると、
0.36 = ( 0.33 )2 = 0.0272 = 0.000729>0.0001
今回は、n = 8 で答の候補が見つかりましたが、もっと大きくなると計算が大変そうです。しかし、2乗の繰り返しならば大きくなるスピードが速いので、 意外と計算の回数は少なくてすみます。試しに、nが選択肢⑤の300より大きくなるまで計算してみます。
0.38 ≒ 0.0001 = 10-4
0.316 = ( 0.38 )2 ≒ ( 10-4 )2 = 10-8
0.332 = ( 0.316 )2 ≒ ( 10-8 )2 = 10-16
0.364 = ( 0.332 )2 ≒ ( 10-16 )2 = 10-32
0.3128 = ( 0.364 )2 ≒ ( 10-32 )2 = 10-64
0.3256 = ( 0.3128 )2 ≒ ( 10-64 )2 = 10-128
0.3512 = ( 0.3256 )2 ≒ ( 10-128 )2 = 10-256
電気通信主任技術者試験では、試験問題に出てくる数値は、ある程度現実性を持たせています。その点で、不信頼度が 10-16 以下は、出題されにくい範囲になります。 つまり、式(26)は試験問題で使われるのは上のほうだけです。したがって、問題を解く際に必要な計算回数もそんなに多くはなりません。
◇例題:装置Aの信頼度が0.8の場合
対数を使わない解法の練習をします。装置Aの信頼度が、0.7ではなく0.8の場合の最小をnを求めます。他の要件は同じです。 この場合は、不信頼度が0.3から0.2に変わります。したがって、不等式(20)は、以下のように変わります。
0.0001 ≧ 0.2n
この式を満たすnを求めてみます。まずは、n = 2 の場合です。
0.22 = 0.04
今度は、残念ながら0.1のようなきりの良い数になりません。しかたがないので、素直にn = 3 を計算します。
0.23 = 0.008 ≒ 0.01
今度は、ほぼ0.01、きりの良い数になりました。一気に、この2乗を計算します。
0.26 = ( 0.23 )2 ≒ 0.012 = 0.0001
正確な不信頼度は、式(30)の近似値よりも小さいので、n = 6 で不等式(27)は正確に成り立ちます。
次は、n = 6 が最小であるかを調べます。そのために、 0.25を、近似抜きで正確に計算してみます。
0.25 = 0.00032>0.0001
したがって、n = 5 では不等式(27)は成り立ちません。これで、n = 6が要件を満たす最小値で確定です。
なお、log10 2= 0.301として正攻法で計算すると、n>5.72です。端数切り上げで6台なので、対数を使わない解法の結果と一致します。
◇近似は、検証にも有効
対数を使わずに、近似を使う解法は、計算結果の検証にも有効です。対数を使った計算は、逆算が難しいので検算も難しくなります。 逆方向の計算ができないならば、別のアプローチの計算方法を使うことにより、計算結果の検証を行うことができます。 対数を使った解法と近似を使った解法を併用することにより、計算ミスを発見しやすくできます。
近似を使った解法は、状況によっては使いにくいケースがあります。たとえば、今回の問題で装置Aの信頼度が0.75の場合、 不信頼度は0.25となりますが、0.25のn乗の計算が簡単にはできません。近似抜きで力ずくで0.25nを計算すれば、答を導けます。 しかし、このような場合には、答の範囲を大ざっぱに絞り込む方法もあります。信頼度を少々さげて信頼度0.7で計算してみるのです。 信頼度0.7で計算して求められた最小台数より大きな数が、信頼度0.75の最小台数になることはあり得ません。構成要素の信頼度が上がったとき、 必要な並列数は、同じかまたは減るかのいずれかです。このように、信頼度0.7で計算すれば最小台数の上限が求められます。さらに、信頼度0.8で計算すれば、最小台数の下限を求めることもできます。
今回は、正攻法の対数を使う方法のほかに、近似を使う方法を説明しました。このパターンに限らず、複数の解法をマスターすれば、 答の検証にも使えます。複数の解法がある計算問題については、できる限り第2の解法も身につけて、点数の取りこぼしを防いでください。